Uppdatering

Det finns några grundläggande frågor. Utgångspunkten för denna idé är att felen i varje mätanordning balanserar, så med tillräckligt med enheter kommer medelvärdet att vara ungefär exakt. Om inte, skulle du åtminstone kunna märka skillnaden mellan de två enheterna och veta när du ska kalibrera om. För vissa typer av mätningar är detta ungefär sant, men för andra är det inte.

Det första stora problemet är att vissa typer av mätanordningar alltid tenderar att drivas i samma riktning. Till exempel, om din enhet jämför en kraft mot en fjäder, kommer våren att bli svagare med tiden när den är trött, aldrig starkare, så dina uppmätta värden kommer alla att glida i samma riktning. Här skulle det inte hjälpa att medelvärdera resultaten från flera enheter, och du skulle inte ens märka felet eftersom fjädrarna kommer att förfalla i ungefär samma takt.

Det andra grundläggande problemet är att även för en mätning där fel var bilaterala och slumpmässiga skulle det krävas många enheter för att vara statistiskt säker på att ditt genomsnitt var bra. Att bara använda två eller tre enheter - alla fel kan mycket väl vara i samma riktning, så ditt genomsnittliga värde skulle fortfarande vara fel. Du behöver många mätanordningar för att få någon precision i ditt genomsnitt.

Förutom dessa två grundläggande principer finns det en massa praktiska skäl att använda kalibrerade mätanordningar när värden betyder något. En är att hantering av provet för att mäta det ett antal gånger skulle ta mer tid, maskiner och / eller hantering vilket ökar kostnaderna och risken för skador. En annan är att för de flesta arbeten som styrs av en standard, kommer enheter att definieras med avseende på ett absolut värde (vanligtvis en fysisk konstant, men ibland en artefakt) och om dina mätningar inte relaterar till det värdet kan du inte vara säker att andra håller med dem. För vissa kritiska arbeten krävs en spårbar släktlinje till en statligt etablerad konstant bakom varje mätning.

Av alla dessa skäl är det nästan alltid bättre att använda ett instrument som regelbundet kalibreras istället för en massa instrument med okänd noggrannhet och försöker få ett statistiskt medelvärde.

Baserat på din redigering tror jag att jag förstår att du inte vill undvika kalibrering helt, bara för att minska frekvensen och minska risken för att ett instrument som kommer ut ur specifikationen (men inom kalibreringsperioden) kommer att leda till ett fel på din slutprodukt. Detta är en bra punkt - det finns en riskanalys att göra för processfel baserat på frekvensen av instrumentfel, frekvensen av kontrollprocessfel och kostnaden för en defekt produkt. Baserat på dessa faktorer kan du lägga till två instrument, varav kanske bara ett är i sin utsedda kalibreringscykel, där det andra bara fungerar som en felmonitor. Om de två instrumenten inte håller med kommer du inte att vara säker på vilket som är rätt, men du vet åtminstone att något går fel och att kontrollera kalibreringen. Det finns inget fel med denna idé, och det kommer förmodligen att hjälpa till att upptäcka några plötsliga fel, även om punkten att vanliga lägesfel inte kommer att upptäckas fortfarande står. Å andra sidan är det förmodligen ingen stor ekonomisk inverkan att hålla båda instrumenten inom sin kalibreringsperiod, (dvs. minska inte kalibreringsintervallet) och då kan du ha mer förtroende för dina resultat.

Ämnet är - som lätt framgår av längden och antalet svar - inte lätt. Det betyder också att det beror mycket på alla specifika fall för att svara på det här ämnet.

Del I:
Om vi ​​definierar att processparametern ($ p $) har som ska övervakas. Mätningen ($ m $) för processparametern innehåller alltid en osäkerhet ($ u $). Så låt oss ange följande modell:

$ m = p + u $

Syftet med varje kalibrering är att specificera osäkerheten. Strikt talat kan osäkerheten bara specificeras för den kalibrering som redan gjorts. Ett mycket rimligt antagande är dock att osäkerheten inte kommer att förändras dramatiskt. Men det kommer att förändras med tiden. Så modellen kommer att se ut så här:

$ m = p + u (t) $

Din föreslagna redundans har olika effekter på osäkerheten, beroende på hur redundans uppnås. Ett sätt kan vara att mäta samma processparameter med en ytterligare sensor av samma typ (1). Ett annat sätt skulle vara att antingen använda en annan sensor (2) eller till och med observera en annan processparameter med en annan sensor (3).

Att bara använda samma sensor för att observera samma parameter kommer sannolikt att ha en liknande försämring av kalibreringskvaliteten. Eftersom orsaken till nedbrytningen inte ändras, så har båda sensorsignalerna möjligen en högre osäkerhet över tiden.

De två andra alternativen har potential att komma med en osäkerhetsmodell som inte skulle göra kalibreringen onödigt men kan öka omkalibreringsperioderna.

Del II:
Det finns i alla fall en betydande skillnad mellan fel och osäkerhet . Om det skulle vara möjligt att veta felet i varje mätning kan man enkelt kompensera för det.
Men det enda en kalibrering kan ge är osäkerheten i en mätning. Eller sätt det tvärtom en kalibrering ger dig en uppskattning av hur säker man kan vara att i (vanligtvis) 95% av alla mätningar kommer det returnerade värdet att vara i det angivna intervallet runt det sanna värdet. Följande bild visar det övre och lägre gränser för osäkerheten förutsatt en mycket enkel nedbrytningsmodell.

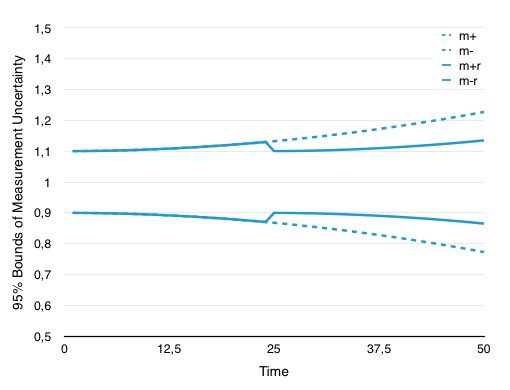
Förutsatt att du vill behålla din processparameter på nivån "1" och din osäkerhet har ett initialvärde på +/- 10% (vilket är enormt men trevligare att illustrera). Anledningen till att du först måste kontrollera parametern är att du måste bevisa att din process (eller produkt) har en specifik kvalitet. Eftersom det lätt kan ses utan omkalibrering (gränser m + och m-, prickade) efter en del imaginär tid har osäkerheten ökat stadigt. Genom att kalibrera om mitt i intervallet minskar du osäkerheten (m + r och mr, fast).

Från din beskrivning antar jag att du måste rapportera eller spara kalibreringen före och efter varje period tillsammans med mätningsloggen för processen för att bevisa din kvalitet under hela produktionscykeln. Det enda sättet att göra det är att samla mer kunskap om denna specifika process.
Just nu är brute-force-metoden att kalibrera två gånger och anta osäkerheten mellan dessa kalibreringar var inom de två kalibreringarna.
Om det skulle vara möjligt att få en bättre modell för osäkerhetsnedbrytningen kan antalet kalibreringar minskas. För att få en bättre modell är det dock nödvändigt att kombinera ett större antal kalibreringar. Ett möjligt sätt kan vara att använda alla tillgängliga kalibreringar och omkalibrering. Det kan vara möjligt att utveckla en bättre förståelse för osäkerheten och därigenom utveckla en bättre modell som skulle förlänga kalibreringsintervallen.

Till exempel med tanke på att sensorerna skulle försämras på det sätt som visas i figuren ovan, en lösning kan vara att ändra kontrollparametrarna för produktionssystemkontrollen över tid. Men sättet att göra detta eller om detta till och med är möjligt beror mycket på din process som vi inte vet ännu.

Slutligen, även om det är kontraintuitivt med redundanta sensorer, minskar inte nödvändigtvis osäkerheten.
Genom att lägga till en extra sensor av samma typ i systemet fördubblar du i princip antalet mätningar och håller samma osäkerhet. Det enda sättet en redundant sensor minskar osäkerheten är när den första sensormätningen inte var representativ för systemet och inte bara hade osäkerhet från sensorn utan ytterligare fluktuationer från själva systemet. Tänk på en mätning som att skjuta mot ett mål. Beroende på dina färdigheter har du en viss sannolikhet att slå bulls eye. Det innebär att genom att skjuta oftare ökar du bara att slå bulls eye men du minskar aldrig spridningen av dina skott. Varje skott har samma sannolikhet att träffa bulls eye. På samma sätt ökar mätningen oftare chansen att mäta det "rätta" värdet, men det är inte intressant här. Det är av intresse hur säker du kan vara att varje uppmätt värde ligger inom ett visst "intervall runt" rätt värde.

Sammanfattar det:

1. Att lägga till sensorer i en mätning minskar inte nödvändigtvis osäkerheten för den kombinerade mätningen.

2. Att ha två sensorer av samma typ ändrar inte nedbrytningshastigheten för det kombinerade mätvärdet jämfört med en enda sensor.

3. Om möjligheten är stor att en sensor skulle ge felaktiga värden under produktionskörningen, än att ha redundanta sensorer är mycket meningsfullt. Men detta har ingenting att göra med värdenas osäkerhet. I det här fallet skulle efterkalibreringen avslöja att processen inte övervakades ordentligt på grund av sensorfel så det finns inget sätt att säkerställa kvaliteten på produktionskörningen alls. I händelse av sensorfel skulle den andra sensorn ha sparkat in och (i bästa fall) gett samma kvalitet som om en sensor skulle ha överlevt hela produktionskörningen.

4. Det enda sättet att minska antalet kalibreringar är att samla alla kalibreringar från det förflutna och försöka bygga en sensor-nedbrytningsmodell utifrån den som kan visa att det nuvarande antalet kalibreringar är onödigt högt.

5. Genom att använda olika sensortyper eller mätning av processparametrar kan det vara möjligt att komma fram till en osäkerhetsmodell som försämras långsammare och är mer robust med avseende på sensorfel.

Att ha två mätanordningar brukar vara en dålig idé för att undvika omkalibrering . Om enheterna ger olika resultat vet du inte vilken som är rätt förrän du kalibrerar om eller gör något felsökning. Naturligtvis säger två olika avläsningar att något är fel med mätsystemet, vilket är mer information än bara en felavläsning.

Om du har tre eller fler enheter, är det ofta förnuftigt att använda "majoritetsröstning" för att bestämma att en enhet ger dålig data och ska ignoreras.

Som andra svar har sagt, måste du också överväga "gemensamt läge" "Orsaker till fel som påverkar varje enhet på samma sätt - inte bara" okontrollerbara "saker som miljöförhållanden, utan också frågor som att använda en gemensam elektrisk strömförsörjning, som kan gå ur specifikationen utan någon indikation och påverka utdata från alla enheter .

Det är alltid en kompromiss. Vanligtvis mellan ekonomi och noggrannhet.

Om du har två temperaturloggare och en faller ur kalibreringen, men du inte vet vilken, har du nu mycket större osäkerheter om dina temperaturobservationer. Och du har två gånger räkningen för omkalibrering.

Det fina med kalibrerat kit är att detta, i de flesta fall, ger dig en ganska rimlig uppfattning om fördelningen av fel på dina observationer, och att gör det mycket lättare att redovisa dem. Att ha N bitar av okalibrerat kit ger dig mycket osäkerhet om vad den faktiska fördelningen av fel är, vilket gör det mycket svårare att hantera dem och redogöra för dem. Så du har ett system där du har betalat extra för redundans, men inte har kompenserat för den minskade noggrannheten.

Om du måste kalibrera varje gång en av dina inspelare inte håller med en annan kan du sluta upp med att göra mer än dubbelt så många omkalibreringar som du gör för närvarande.

Och om de två inspelarna avlägsnar kalibreringen, men synkroniseras med varandra, kommer du att sakna en kritisk omkalibrering. Och att förstå fördelningen av sådana vanliga fel är verkligen svårt; så återigen har du ingen känd felfördelning som du kan mäta och hantera; istället har du en okänd felfördelning, vilket ökar dina kostnader.

Mer oberoende mätningar med samma noggrannhet ändrar bara sannolikhetsprofilen för felet, inte det värsta fallet.

Ett bra exempel är att kasta två tärningar. Du kan betrakta varje matris som ett medelvärde på 3,5 ± 2,5. Vilken som helst rulle med valfri munstycke kan vara var som helst i det intervallet med lika sannolikhet. Men genomsnittet av två tärningar har en triangulär profil. Sex olika möjliga kombinationer resulterar i 3,5, medan endast en kombination vardera resulterar i 1 eller 6.

Att kasta fler tärningar minskar sannolikheten för genomsnittet runt 3,5, men sannolikheten för 1 eller 6 går aldrig till 0. Det värsta fallet är fortfarande detsamma som tidigare. Ingen mängd extra tärningar kan förändra det värsta fallet.

Eftersom vi för det mesta för produktionsmätningar bryr oss om värsta fallet, hjälper flera mätningar inte.

, notera att det bättre genomsnittliga fallet för flera tärningar bara fungerar eftersom varje mätning (varje form) är oberoende av de andra. Samma mätprocess, även utförd oberoende av olika instrument, kan ha några vanliga felkällor. Till exempel kan temperatur, atmosfärstryck, ålder osv. Alla påverka olika instrument som mäter samma sak på samma sätt.

Det är sällsynt att du får riktigt oberoende mätningar och då blir du bara bättre genomsnittligt svar, inte ett värsta fall i alla fall.