Även om den här strålen presenterar fem begränsningar ( $ X_A $ , $ Y_A $ , $ M_A $ , $ Y_F $ , $ Y_G $ ) , det är faktiskt statiskt bestämt. En statiskt obestämd struktur är en där det finns fler okända (begränsningar, i detta fall) än det finns statiska jämviktsekvationer. Vanligtvis har man tre ekvationer: $ \ sum F_X = 0 $ , $ \ sum F_Y = 0 $ , $ \ sum M_? = 0 $ (där $? $ är någon godtycklig punkt). Gångjärn ger oss dock en extra ekvation: $ \ sum M_ {h \ pm} = 0 $ , där $ h \ hspace {-2pt} \ pm $ är en sida av gångjärnet (vänster eller höger), som i den här frågan. Detta skiljer sig från den globala nollböjningsmomentekvationen som tar hänsyn till alla krafter på vardera sidan om gångjärnet. Lägga till de två ytterligare ekvationerna som ges av gångjärnen vid $ C $ och $ E $ till de tre globala jämvikten ekvationer, vi har därför lika många ekvationer som vi har begränsningar (5), och kan därför lösa detta problem på traditionellt sätt.
Med detta sagt finns det en mycket lättare sätt att göra detta som är helt praktiskt, utan beräkningshjälpmedel .
För detta praktiska tillvägagångssätt måste man observera det dubbla gångjärnet i span $ \ overline {CE} $ . Detta innebär att böjmomentet vid $ C $ och $ E $ måste vara noll, ungefär som med en helt enkelt stödjad stråle (en djupare förklaring av varför denna jämförelse är giltig kan ses i slutet).
Så låt oss ersätta den strålen med följande bitar (lägg märke till att belastningarna vid $ C $ och $ E $ lämnas tomma för tillfället):
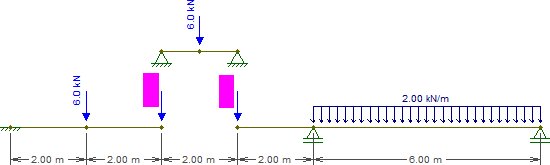
Lösa strålen som representerar $ \ överliggande {CE} $ är trivialt. För närvarande är allt vi behöver reaktionerna, som är lika med $ 3 \ text {kN} $ vid varje support.
Få nu dessa reaktioner och kasta ner dem till de andra bitarna, kom ihåg att vid $ C $ finns också den koncentrerade $ 2 \ text {kN} $ kraft, som måste läggas till. Vi har därför:
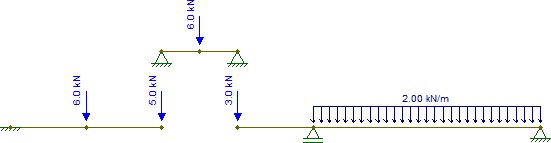
De andra delarna är också isostatiska och kan löses trivialt (förutsatt att man vet hur man får interna isostatiska krafter strukturer). De resulterande interna krafterna är (jag ändrade stödet vid $ G $ bara för att göra den biten stabil för horisontella krafter, vilket inte ändrar något i det här fallet):
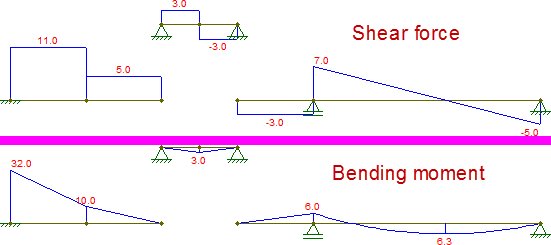
När de bildar dessa diagram är de identiska med dem som erhållits med den ursprungliga strålen:
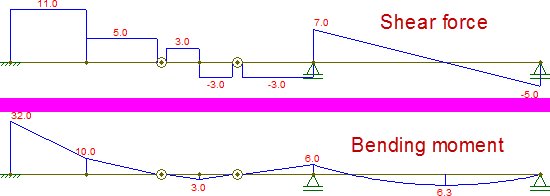
En enkel anledning till varför jämförelsen kan göras mellan de dubbla gångjärnen och en enkelt stödd stråle är att det här är grundprincipen bakom Gerber-strålar (vilket i princip är vad $ \ overline {CE} $ representerar). De är balkar som vilar på andra balkar (se exempel här, där balkarna till höger och vänster är Gerber-balkar) och som därför kan "lyftas" från resten av strukturen, lösas och sedan har deras reaktioner distribuerats till resten av strukturen. Man behöver inte oroa sig för påverkan av externa krafter eller närliggande balkar som överför skjuvkrafter på grund av det faktum att böjningsmomentet måste vara noll vid varje extremitet av Gerber-strålen. Detta innebär att skjuvets integral längs Gerber-strålen måste vara noll, vilket bara kan uppstå om endast belastningarna i strålen och reaktionerna vid dess extremiteter beaktas.
Programmet jag använde för dessa diagram var Ftool, ett gratis 2-D-ramanalysverktyg.