I allmänhet består varje tand i ett involverat kugghjul av två kurvor: den involverade kurvan och rotfilén. Den involverade kurvan är avgörande för att kugghjulen ska fungera korrekt och gör att kraften kan överföras smidigt från en växel till den andra. Rotfilén å andra sidan är inte direkt inblandad i kraftöverföring eller kugghjulens kinematik (dvs. hur en växels rörelse påverkar rörelserna hos ett kugghjul.). Detta betyder att rotfilékurvens form är rimligt godtycklig, förutsatt naturligtvis att rotfilén på ena växeln inte vid någon tidpunkt kommer i kontakt med tänderna på den andra växeln. Dessutom spelar rotfilén en roll för att bestämma hur mycket böjspänning som utvecklas vid tänderoten under operation: om rotfilén har en låg krökningsradie kommer detta att resultera i en stor spänningskoncentration vid roten. / p>
Trots att rotfilékurvan har potential att vara nästan vilken form som helst, finns det några former som förekommer vanligt, de två som jag tror är vanligast är följande:
1. Anslutning av involverad kurva och rotcirkel med radiella linjer
Den enklaste rotfilén för matematisk bestämning är helt enkelt en rak radiell linje som förbinder början av involveringskurvan till rotcirkeln. Detta visas nedan:
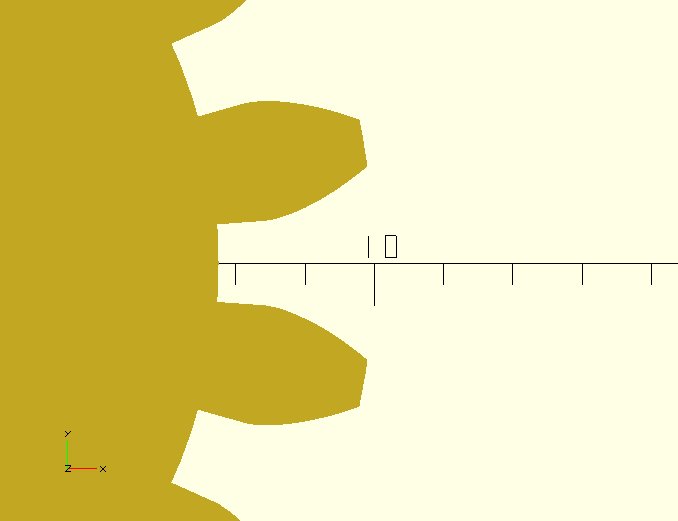
Fördelarna med roten "filé" (ett skarpt hörn är inte mycket av en filé antar jag) är att geometrin är väldigt enkel. Det finns dock två stora nackdelar: 1. Det skarpa hörnet ger en mycket stor spänningskoncentration vid växelns rot, vilket betyder större rotböjningsspänningar. Detta innebär att dessa växlar inte är lämpliga för applikationer som utsätter dem för starkt vridmoment. 2. I fall där störningar under underskott blir ett problem, kommer dessa radiella linjer att komma i vägen för tänderna och orsaka att kugghjulen fastnar. För kugghjul med tryckvinklar vid standardvärdet 20 ° uppträder vanligtvis underskurna störningar för kugghjul med kuggar mindre än 18 (om kugghjulet är i ingrepp med ett kuggväxel) eller 13 (om kugghjulet krossar ett annat kugghjul med lika antal tänder) . Av dessa anledningar ser du sällan växlar med denna typ av rotfilé i industriell tillämpning, men är vanligtvis fina i områden där tandantalet är ganska högt och kugghjulen inte utsätts för höga vridmoment.
2. Trochoidal rotfilé
En av de vanligaste processerna för att generera spindelväxlar och spiralformade växlar är hobbing, och rotfilén som naturligt produceras som ett resultat av hobbing är den trochoidala kurvan. Ett exempel på ett kugghjul med trochoidformade rotfiléer visas nedan:
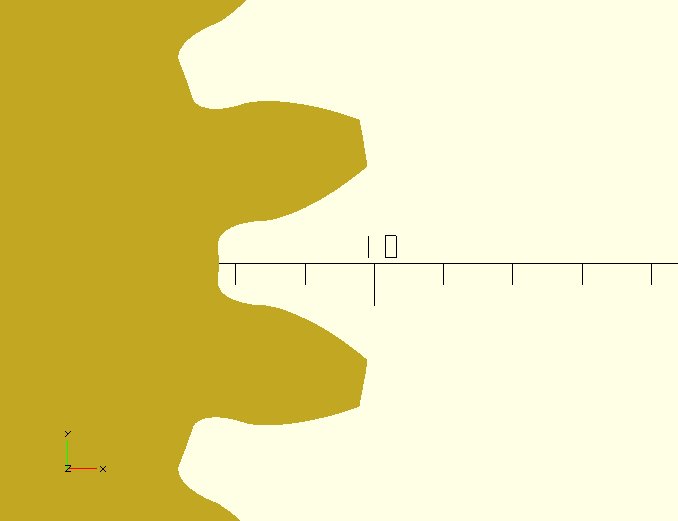
Den enskilda trochoidala kurvan och den involverade kurvan visas tillsammans med roten cirkel och yttre cirkel enligt nedan:
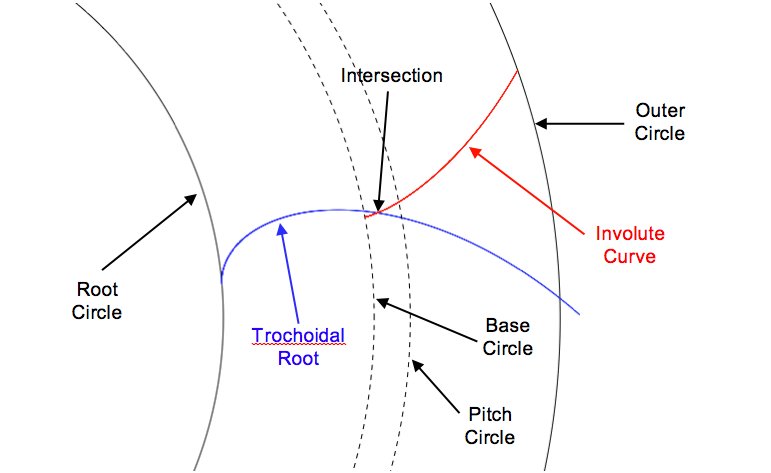
Det första som ska märkas är att den trochoida filén är avsevärt mer avrundad än det tidigare fallet, så att mindre böjspänning kommer att utvecklas vid tandens rot och så att växeln är mer lämplig i högmomentscenarier. Lägg också märke till hur den trochoidala kurvan skär sig med den involverade kurvan vid en punkt något till höger om början av involuten: en del av den involverade kurvan har oavsiktligt tappats av hobbeprocessen! Ju mindre antal tänder, desto större blir denna involverade förlust, och det blir uppenbart när störningar på underskäret börjar inträffa: i ett sådant fall sägs kugghjulen vara underskuren . Medan för radiallinjefilettkurvor den underskurna störningen skulle ha orsakat att kugghjulen fastnat, kommer kugghjul med trochoida filéer inte att klämma fast under sådana omständigheter.
När kugghjulen skapas genom hobbing är det som om ett rack kugghjulet rullar längs ett kugghjulsmaterial (cirkel med en diameter lika med kuggtandens yttre diameter), där materialet subtraheras varhelst kugghjulet har varit. Nedanstående animation ska illustrera hur rackväxeln kan generera formen på en spindelväxel med trochoidfiléer:

Lägg märke till hur tänderna på rackkugghjulet är trapesformat (och även att kuggkugghjulet här, som en skärare, har ett tillägg på $ 1,25m $ och ett dedement på $ m $, till skillnad från vanliga rackkugghjul), och skärning av dessa trapeziumtänder i ett redskap blank lyckas magiskt skapa två kurvor, de involverade och de trochoidala kurvorna. Mer exakt genereras den involverade kurvan av någon av trapezins diagonala linjer, och den trochoida kurvan genereras av någon av de två punkterna i trapezens ände. Med denna information är det möjligt att uttrycka den trochoida filén som en parametrisk ekvation.
Nästa avsnitt i denna fråga kommer att titta på matematiken bakom härledningen av en sådan parametrisk ekvation.
Hämta den trochoidala kurvan
Låt oss först och främst överväga en enda trapets av kuggväxeln och se hur en punkt i slutet av ett trapets rör sig i förhållande till kugghjulet som skärs. Kurvan som denna punkt följer blir den trochoidala kurvan. Stegpunkten för trapeset, $ P $, är den punkt på trapetset som initialt kommer att ligga på redskapens stigningscirkel, som visas nedan.
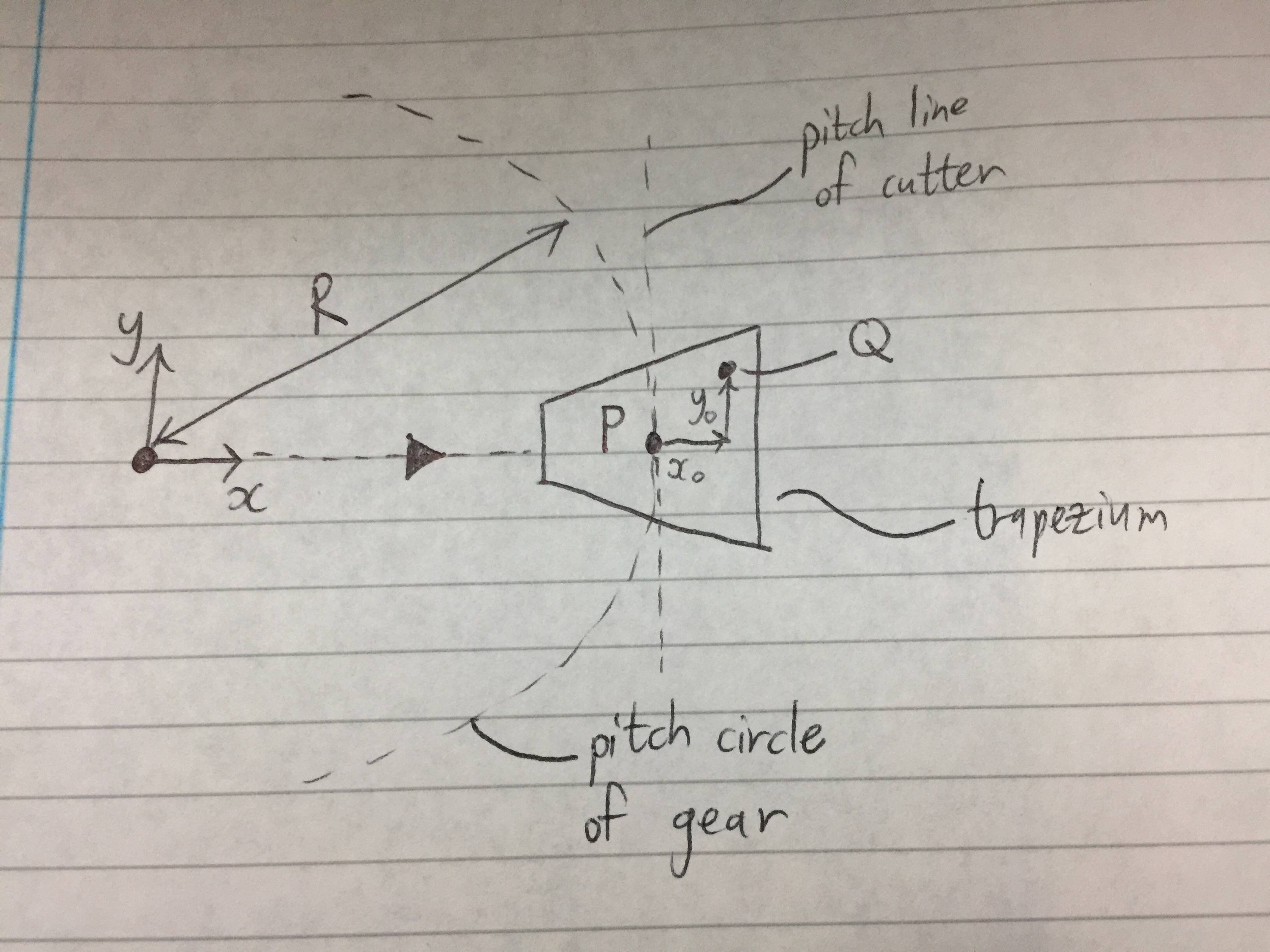
Observera att radien för tonhöjdscirkeln är $ R $, och att det finns en allmän punkt $ Q $ som ligger på trapeset, förskjuten från $ P $ med $ x_0 $ och $ y_0 $ i $ x $ och $ y $ riktningar (senare kommer vi att ställa in den här punkten som en av punkterna i slutet av trapeset). Observera också den heldragna svarta triangeln: detta är för att identifiera redskapets orientering. Den nuvarande positionen för $ Q $ kan uttryckas enligt följande:
$$ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ börja {array} {c} R + x_0 \\ y_0 \ end {array} \ right] $$
Låt oss nu rotera växeln moturs med en vinkel $ t $, som sedan skjuter trapeziet uppåt efter avstånd $ Rt $ (ingen glidning mellan tonhöjdscirkel och tonhöjdslinje). Illustration:
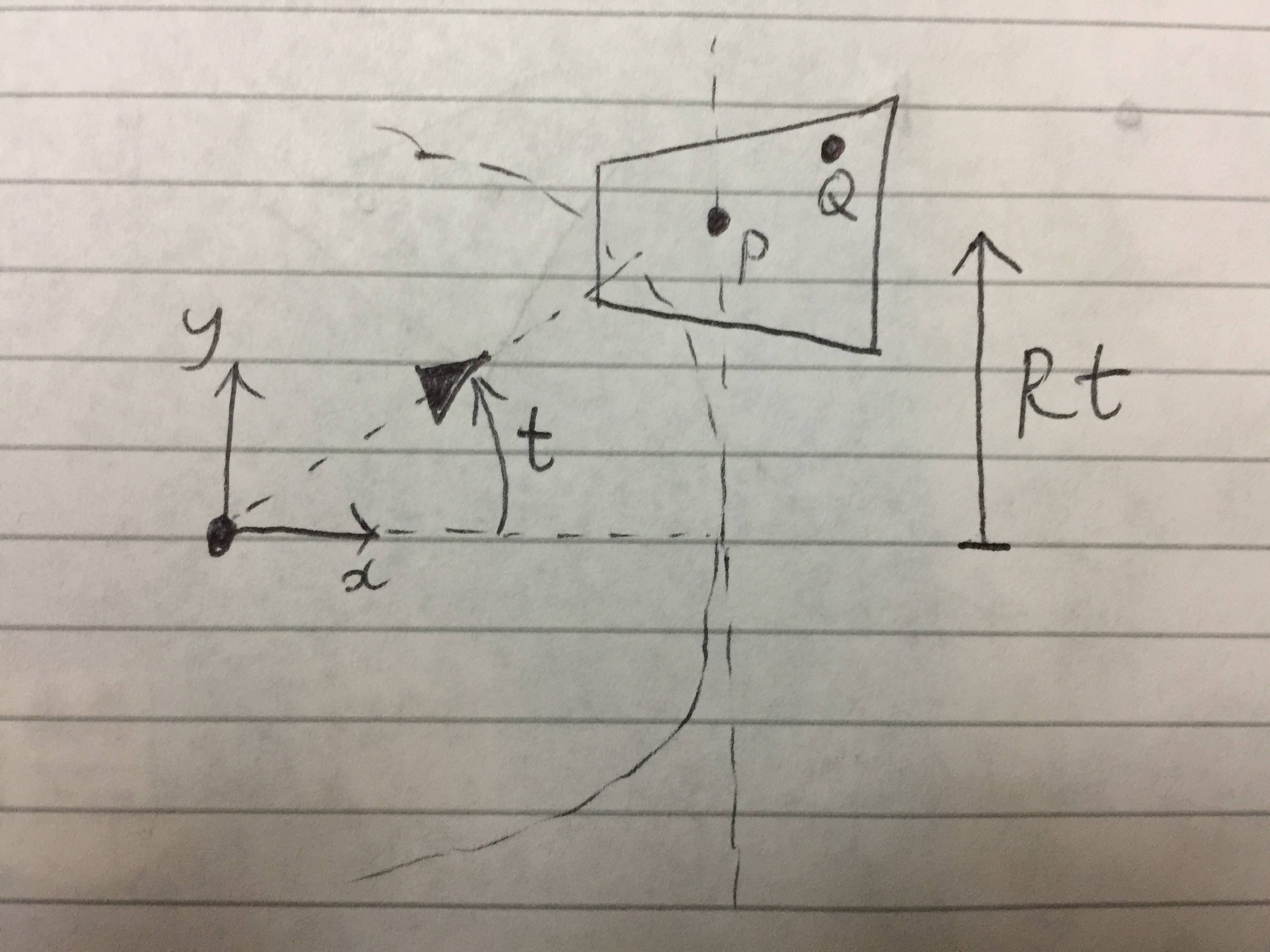
Lägg märke till hur den helt svarta triangeln har rört sig i enlighet med växeln. Positionen för $ Q $ är nu:
$$ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {c} R + x_0 \\ Rt + y_0 \ end {array} \ right] $$
Trapeset har flyttat, men det har också växeln: vi är intresserade av rörelsen på $ Q $ relativt till redskapet. Därför måste vi rotera hela systemet om ursprunget med vinkel $ t $ medurs. Detta roterar helt enkelt perspektivet så att det återställer växeln till sitt standardläge samtidigt som den nya rörelsen för trapeziet bibehålls, dvs vi får rörelsen av ett trapezium när racket rullar runt det stationära kugghjulet, liknande animationen ovan.
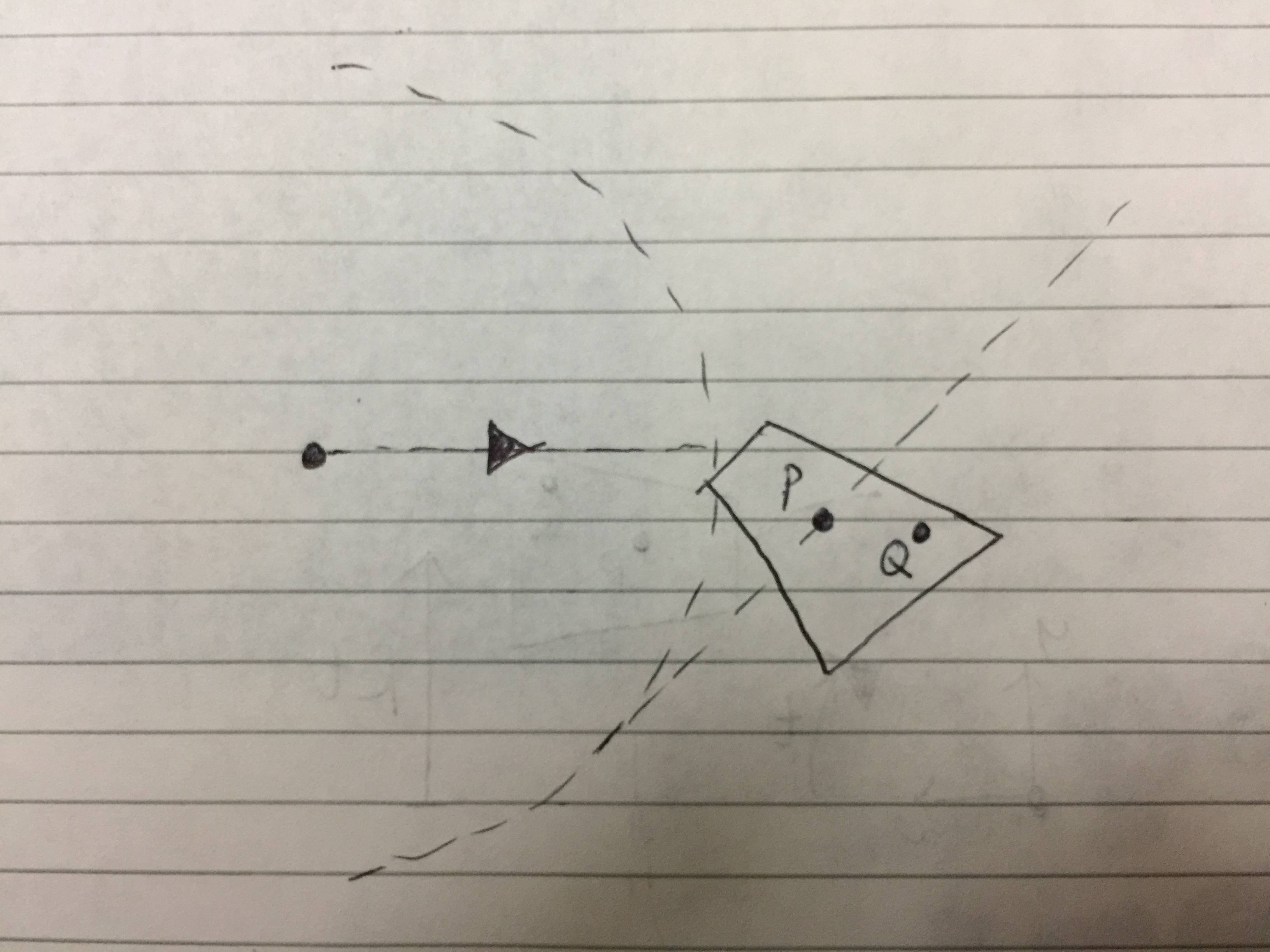
För att få positionen för punkten $ Q $ måste vi multiplicera den tidigare positionen med en rotationsmatris medurs, så positionen uttrycks som följer:
$$ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ begin {bmatrix} \ cos {t} & \ sin {t} \\ - \ sin {t} & \ cos {t} \ end {bmatrix} \ left [\ begin {array} {c} R + x_0 \\ Rt + y_0 \ end {array} \ right] = \ left [\ begin {array} {c} (R + x_0) \ cos {t} + (Rt + y_0) \ sin {t} \\ - (R + x_0) \ sin {t} + (Rt + y_0) \ cos {t} \ end {array} \ right] $$
Slutligen, genom att ställa in $ Q $ som "övre vänstra" punkt på trapeset, dvs $ x_0 = -1,25m $ och $ y_0 = \ frac {1 } {4} \ pi m - 1,25m \ tan {\ phi} $, där $ \ phi $ är tryckvinkel, och noterar också att $ R = \ frac {1} {2} Nm $, där $ N $ är antal kuggar, du får den parametriska ekvationen för den trochoidala filetkurvan:
$$ \ left [\ begin {array} {c} x (t) \\ y (t) \ end {array } \ right] = \ left [\ begin {array} {c} (\ frac {1} {2} Nm-1.25m) \ cos {t} + (\ frac {1} {2} Nmt + \ frac {1 } {4} \ pi m - 1.25m \ tan {\ phi}) \ sin {t} \\ - (\ frac {1} {2} Nm-1.25m) \ sin {t} + (\ frac {1 } {2} Nmt + \ frac {1} {4} \ pi m - 1,25m \ tan {\ phi}) \ cos {t} \ end {array} \ right] $$
Observera att parametern $ t $ börjar på $ t = - \ frac {y_0} {R} = - \ frac {\ frac {1} {4} \ pi - 1.25 \ tan {\ phi}} {\ frac {1} {2} N} $ och ökar upp till ett visst värde som representerar korsningen av trochoiden med den involverade.
Hoppas att svarar på din fråga :)