Utan mer info tror jag att ditt problem härrör från värdena för $ a_0 $ och $ a_1 $ span>. Svaret är lite inblandat, så lite systembakgrund är nödvändig.

Det korta svaret

Ditt system ska vara stabilt, men jag tror inte att du simulerar ditt system tillräckligt länge för att se att den stabiliseras. Beräkna din avvecklingstid och simulera den åtminstone så länge för att se hela svaret övergående.

Det långa svaret

Den karakteristiska ekvationen (dvs. nämnaren för överföringsfunktionen) för en allmän Andra ordningens system har följande praktiska form:

$ s ^ 2 + 2 \ zeta \ omega_n s + w_n ^ 2 $

I det här formuläret är $ \ zeta $ känt som dämpningsförhållandet och $ \ omega_n $ är den naturliga frekvensen. Som du noterade är detta system garanterat stabilt om $ w_n ^ 2 > 0 $ och $ 2 \ zeta \ omega_n > 0 $ .

Inom systemteknik har vi flera tumregler för att bestämma det övergående svaret för sådana system. En av dessa kallas avvecklingstiden $ t_s $ . Det är ett mått på hur lång tid det tar för amplituden för systemets svängningar att sjunka under ett visst tröskelvärde, vanligtvis 2% eller 5% av steady state-värdet (dvs. det värde som systemet stabiliseras med). Du kan beräkna din avvecklingstid med följande approximation (den här är för 2% -kriteriet):

$ t_s = \ frac {4} {\ zeta \ omega_n} $

Om du inte simulerar ditt system förrän avvecklingstiden kan du se ett system som inte verkar stabilisera. Observera att om $ \ omega_n $ är väldigt liten (därför är $ a_0 $ parametern väldigt liten) lösningstiden kan vara mycket lång.

För din referens kan du beräkna $ \ omega_n $ och $ \ zeta $ från dina parametrar via följande:

$ \ omega_n = \ sqrt {a_0} \ qquad \ zeta = \ frac {a_1 } {2 \ omega_n} $

En demonstration

Kolla in vad som händer när jag simulerar ett andra ordenssystem med $ \ omega_n = 0,01 $ rad / s och $ \ zeta = 0,9 $ (dvs. $ a_0 = 0,0001 $ och $ a_1 = 0.0180 $ ). Dess sedimenteringstid är ungefär 444 sekunder. De initiala villkoren är $ \ phi = 0 $ och $ \ frac {d \ phi} {dt} = 0 $ . Jag applicerade en enhetsstegsingång (dvs. en konstant motoringång lika med 1). Följande figurer visar samma system med exakt samma förhållanden, men simuleras under olika tidsperioder. Allt detta gjordes i MATLAB Simulink, min föredragna matte-simulator.

Som du kan se på den första bilden verkar det som om mitt system är instabilt, men i den andra bilden blir det klart att det helt enkelt tar mycket lång tid att stabilisera sig.

Jag hoppas det här hjälper.

Jag är också en mjukvarukille och inte helt ämnet, men jag försökte modellera ditt system. Varje steg visas så att du kan fånga misstag som jag gjorde.

Här är det schematiska diagrammet för likströmsmotorn: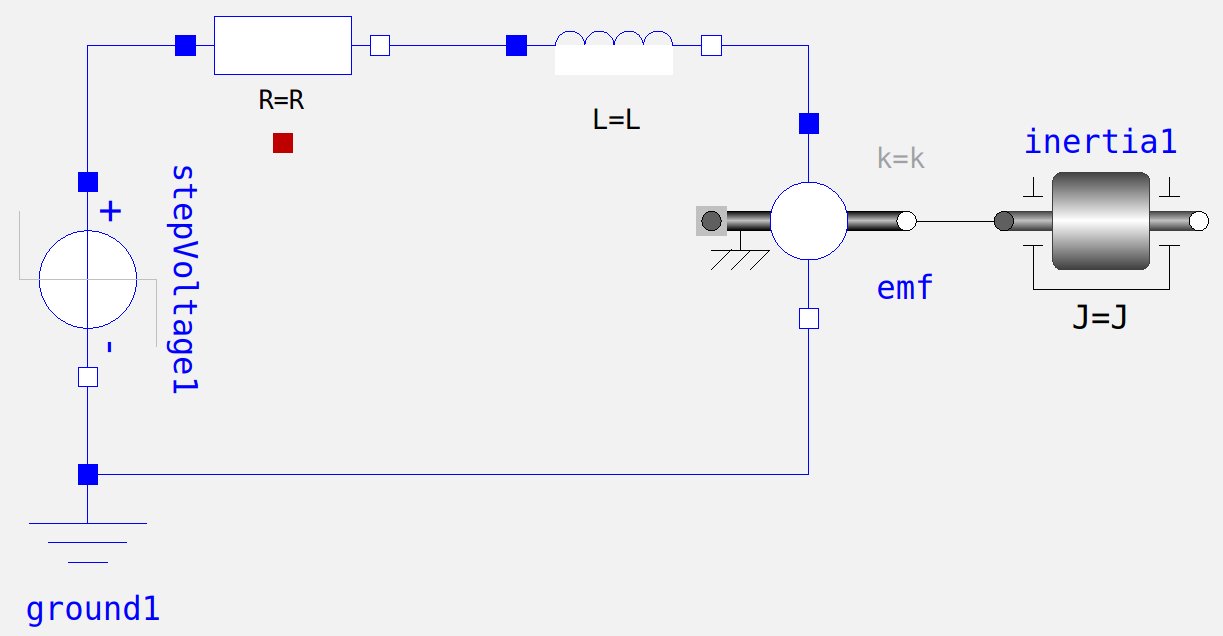

Kirchoffs spänningslag för elektrisk krets: \ begin {ekvation} \ etikett {eq: kirchoff} \ tag {1} V_s = V_l + V_r + V_e \\\ slut {ekvation}

Newtons $ 2 ^ {nd} $ lag rörelse: \ begin {ekvation} \ etikett {eq: newton} \ tag {2} \ sum {F} = ma \ end {ekvation}

Ekvation för elektromotivkraft (EMF): \ börja {ekvation} \ label {eq: emf} \ tag {3} V_e = K_e \ dot {\ theta} \ end {ekvation}

Ekvation för elektromekanisk omvandling av turque: \ begin {ekvation } \ label {eq: torque} \ tag {4} \ tau = K_ti \ end {ekvation}

Använda ekvationer \ ref {eq: kirchoff} & \ ref {eq: emf}: $$ u (t) = L \ frac {di} {dt} + R i + K_e \ dot \ theta $$

Använda ekvationer \ ref {eq: newton} & \ ref {eq: vridmoment}: $ $ K_t i = J \ ddot \ theta $$ Laplace-överföring av ekvationer: $$ U (s) = s LI (s) + RI (s) + s K_e \ Theta (s) \\ K_t I (s) = s ^ 2 J \ Theta (s) $$$ I (s) $ är vanligt: ​​$$ I (s) = \ frac {U (s) - s K_e \ Theta (s)} {s L + R} \\ I (s) = \ frac {s ^ 2 J \ Theta (s)} {K_t} $$

$$ \ frac {U (s) - s K_e \ Theta (s)} {s L + R} = \ frac {s ^ 2 J \ Theta (s)} {K_t} \\ K_t U (s) - s K_t K_e \ Theta (s) = s ^ 3 JL \ Theta (s) + s ^ 2 JR \ Theta (s) \\ K_t U (s) = s ^ 3 JL \ Theta (s) + s ^ 2 JR \ Theta (s) - s K_t K_e \ Theta (s) \\ K_t U (s) = \ Theta (s) (s ^ 3 JL + s ^ 2 JR - s K_t K_e) $$

Överföringsfunktion för system med spänningsingång och positionsutgång: $$ \ frac {\ Theta (s)} {U (s)} = \ frac {K_t} {s ^ 3 JL + s ^ 2 JR - s K_t K_e} $$

Om vi ​​vill undersöka spänningshastighetsförhållandet: $$ s (\ frac {\ Theta (s) } {U (s)}) = s (\ frac {K_t} {s ^ 3 JL + s ^ 2 JR - s K_t K_e}) \\\ frac {s \ Theta (s)} {U (s)} = \ frac {K_t} {s ^ 2 JL + s JR - K_t K_e}) $$

Tillämpar steginmatning, vilket är PWM med 100% arbetscykel: $$ \ Theta (s) = \ frac {\ alpha} {s} \ frac {K_t} {(s ^ 3 JL + s ^ 2 JR - s K_t K_e)} $$

Det kan vara bra att undersöka stabiliteten i ett system med impulsinmatning istället för steginmatning.

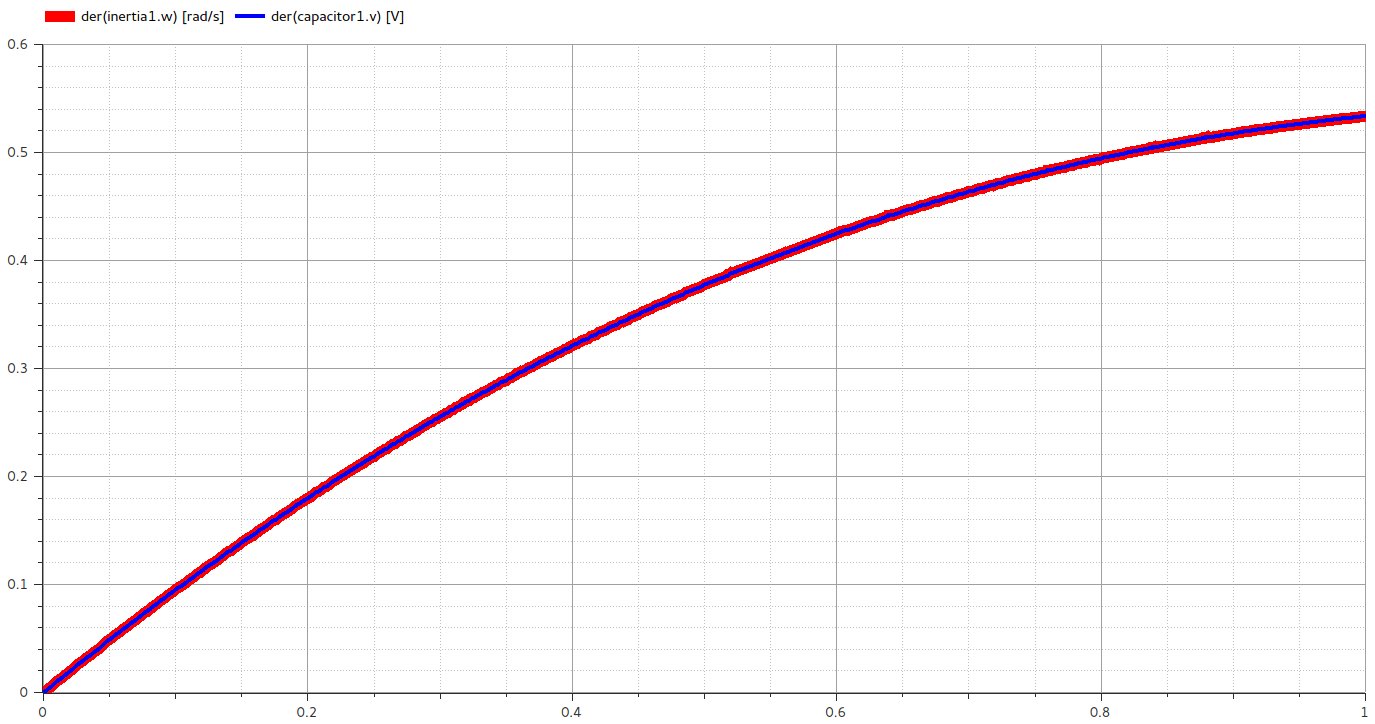
Med mobilitetsanalogi är Voltage & Velocity korsvariabler, Current & Force är genom variabler, du kan också undersöka systemet som RLC-seriekrets som visas nedan.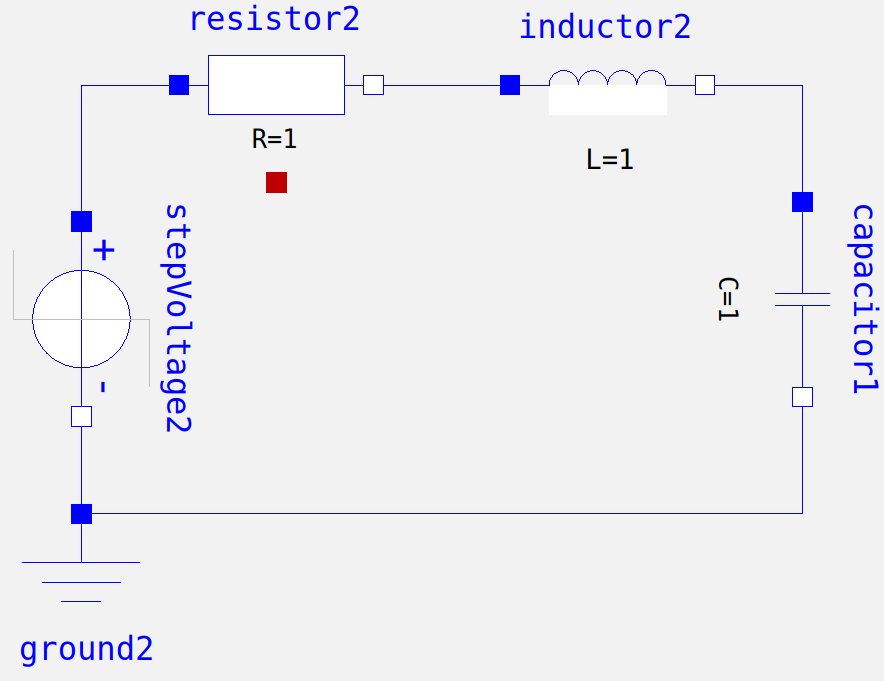

För $ u (t) $ input $ V_c $ output är det spänningshastighetsrelation och $ u (t) $ input $ \ int {v_c (t) dt} $ för spännings-positionsrelation. Så det lägger till ytterligare 1 grad till ditt system.